

Нет предела разнообразию кроссвордов
Классификация кроссвордов
Со времени появления на свет первого кроссворда прошло уже много лет и все это время кроссворд, как говорят, "жил и развивался". На сегодняшний день тот первый кроссворд дал такое многочисленное "потомство", что в одной статье их все описать просто невозможно. Поэтому остановлюсь лишь на некоторых, более менее основных, видах кроссвордов. Да и то, пока только классических. Остальные виды буду разбирать по косточкам в следующих статьях.
Начнем мы этот небольшой обзор с того, что объединим существующие ныне, как уже говорилось выше, более менее основные виды кроссвордов на четыре группы, группируя их. кроссворды, по следующим признакам:
Первая группа. В нее входят виды кроссвордов, имеющие какие-то общие признаки, касающиеся, так сказать, "игрового поля". Или, проще, сетки.
Сюда входят кроссворды с привычными нам черными и белыми клетками, без черных разделительных клеток, симметричные (по горизонтали, по вертикали, круговая симметрия), не симметричные, фигурные.
Вторая группа. Сюда мы занесем те кроссворды, которые объединяют некие общие способы вписывания слов в сетку (заполнения).
Это кроссворды, в которых имеются вопросы-определения к словам, и без таковых, где не требуются особые знания, зато включается логика. Сюда же отнесем кроссворды с привычным нам способом заполнения, то есть начиная из левого верхнего угла, и, так сказать, реверсивные, где слова могут вписываться в сетку в любых направлениях и даже изгибаться (например, так называемые, венгерские кроссворды).
Третья группа. В эту группу входят кроссворды с общими признаками особенностей подбираемых составителями определений к словам.
Это прямые вопросы, где на конкретный вопрос нужно дать конкретный ответ. Это ассоциативные определения, где ответ находится по ассоциации с вопросом, цитатные, где дается известная фраза с пропущенным словом. Это кроссворды с фрагментами, где вместо определений к словам даются картинки, ребусы и т.п. Сюда же входят кроссворды с определениями разных уровней сложности.
Четвертая группа. В последнюю, четвертую, группу мы отнесем все остальные кроссворды, которые не вписываются в предыдущие три.
Это кроссворды, сходные по типам пересечения слов. Например, классические, в которых, соответственно, классический вид пересечений. Так называемые итальянские (иногда их называют американскими), в которых слова могут идти в любом направлении, в том числе и по диагонали. Венгерские, где слова вообще не пересекаются, изгибаясь при этом во все четыре стороны. Ну и двойной линейный, в котором начало каждого очередного слова - это окончание предыдущего.
В эту же группу входят кроссворды, объединяемые некими общими условиями. Например, все слова должны начинаться с одной буквы. Или все слова должны быть одной длины. Ну и так далее.
Теперь чуть подробнее остановимся на некоторых из разновидностей, о которых упоминалось выше.
Начнем мы этот небольшой обзор с того, что объединим существующие ныне, как уже говорилось выше, более менее основные виды кроссвордов на четыре группы, группируя их. кроссворды, по следующим признакам:
Первая группа. В нее входят виды кроссвордов, имеющие какие-то общие признаки, касающиеся, так сказать, "игрового поля". Или, проще, сетки.
Сюда входят кроссворды с привычными нам черными и белыми клетками, без черных разделительных клеток, симметричные (по горизонтали, по вертикали, круговая симметрия), не симметричные, фигурные.
Вторая группа. Сюда мы занесем те кроссворды, которые объединяют некие общие способы вписывания слов в сетку (заполнения).
Это кроссворды, в которых имеются вопросы-определения к словам, и без таковых, где не требуются особые знания, зато включается логика. Сюда же отнесем кроссворды с привычным нам способом заполнения, то есть начиная из левого верхнего угла, и, так сказать, реверсивные, где слова могут вписываться в сетку в любых направлениях и даже изгибаться (например, так называемые, венгерские кроссворды).
Третья группа. В эту группу входят кроссворды с общими признаками особенностей подбираемых составителями определений к словам.
Это прямые вопросы, где на конкретный вопрос нужно дать конкретный ответ. Это ассоциативные определения, где ответ находится по ассоциации с вопросом, цитатные, где дается известная фраза с пропущенным словом. Это кроссворды с фрагментами, где вместо определений к словам даются картинки, ребусы и т.п. Сюда же входят кроссворды с определениями разных уровней сложности.
Четвертая группа. В последнюю, четвертую, группу мы отнесем все остальные кроссворды, которые не вписываются в предыдущие три.
Это кроссворды, сходные по типам пересечения слов. Например, классические, в которых, соответственно, классический вид пересечений. Так называемые итальянские (иногда их называют американскими), в которых слова могут идти в любом направлении, в том числе и по диагонали. Венгерские, где слова вообще не пересекаются, изгибаясь при этом во все четыре стороны. Ну и двойной линейный, в котором начало каждого очередного слова - это окончание предыдущего.
В эту же группу входят кроссворды, объединяемые некими общими условиями. Например, все слова должны начинаться с одной буквы. Или все слова должны быть одной длины. Ну и так далее.
Теперь чуть подробнее остановимся на некоторых из разновидностей, о которых упоминалось выше.
Кроссворд "Классический"
Старый добрый интеллектуальный классический кроссворд без особых изысков. Сетки в таких кроссвордах обычно симметричны, реже - асимметричны. Причем хорошим тоном считается разумная асимметрия, не режущая глаз своей хаотичностью. Так же одно из правил гласит, что количество черных клеток должно быть меньше, чем белых, а каждое слово должно пересекаться с другими не менее. чем на 60%. Чуть ниже вы видите примеры описанных сеток:
Старый добрый интеллектуальный классический кроссворд без особых изысков. Сетки в таких кроссвордах обычно симметричны, реже - асимметричны. Причем хорошим тоном считается разумная асимметрия, не режущая глаз своей хаотичностью. Так же одно из правил гласит, что количество черных клеток должно быть меньше, чем белых, а каждое слово должно пересекаться с другими не менее. чем на 60%. Чуть ниже вы видите примеры описанных сеток:

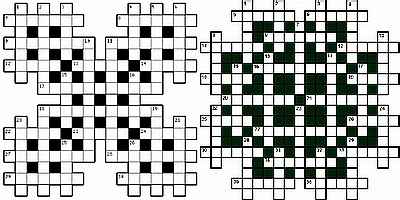
Разумная асимметрия сетки
Хорошая классическая сетка
Переизбыток черных клеток
Кроссворд "С фрагментами"
Это, в принципе, все тот же классические кроссворд, за исключением того, что вместо определений к словам здесь даны какие-то рисунки. Вписывать в сетку нужно названия того, что изображено на этих рисунках, либо некий фрагмент на рисунке, либо год изображенного события и т.д., и т.п. В этих случаях к рисунками даются поясняющие подписи. Чтобы было понятнее, о чем вообще идет речь, вспомните кроссворды с фрагментами, которые в советкое время печатались в журнале "Наука и жизнь":
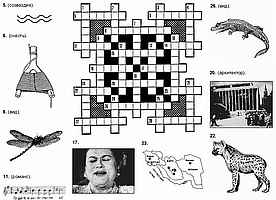
Кроссворд "С фрагментами" из журнала "Наука и жизнь"
Кроссворд "По местам"
Дается сетка с сопроводительным списком всех ответов. Ответы рассортированы по длине слов и по алфавиту. Задача - заполнить сетку кроссворда словами из этого списка. Для усложнения задания в этот список иногда добавляется лишнее слово. Которое, кстати, может выступать в роли призового слова.
* Числобус
Иногда его еще называют "Шифробус". Здесь нет определений к словам, зато в каждой клетке стоят цифры, которые соответствуют определенным буквам, причем одинаковые буквы заменены одинаковыми цифрами. В роли подсказки обычно выступает какое-нибудь слово, изначально вписанное в сетку числобуса.
Кроссворд "Алфавитный"
Здесь все просто - все ответы должны начинаться с одной и той же буквы. Такой кроссворд, как правило, разгадывается чуть легче обычного за счет имеющихся подсказок в виде заранее известной первоначальной общей букве. Если только составитель не придумает к словам мудреные определения.
Кроссворд "Фигурный"
Само название уже дает нам представление о чем здесь идет речь. Как правило, вся "фигуристость" здесь сводится к макетированию сетки кроссворда в виде какой-нибудь несложной фигуры: собачка, машинка, елочка, ракета и т.п. В остальном же это обычный классический кроссворд.
Гораздо реже встречается фигурные кроссворды другого типа: диагональные, сотовые, круговые и т.п. Почему? Да потому, что их труднее составлять. Чуть ниже показаны сетри трех таких "крученых" кроссворда:
Дается сетка с сопроводительным списком всех ответов. Ответы рассортированы по длине слов и по алфавиту. Задача - заполнить сетку кроссворда словами из этого списка. Для усложнения задания в этот список иногда добавляется лишнее слово. Которое, кстати, может выступать в роли призового слова.
* Числобус
Иногда его еще называют "Шифробус". Здесь нет определений к словам, зато в каждой клетке стоят цифры, которые соответствуют определенным буквам, причем одинаковые буквы заменены одинаковыми цифрами. В роли подсказки обычно выступает какое-нибудь слово, изначально вписанное в сетку числобуса.
Кроссворд "Алфавитный"
Здесь все просто - все ответы должны начинаться с одной и той же буквы. Такой кроссворд, как правило, разгадывается чуть легче обычного за счет имеющихся подсказок в виде заранее известной первоначальной общей букве. Если только составитель не придумает к словам мудреные определения.
Кроссворд "Фигурный"
Само название уже дает нам представление о чем здесь идет речь. Как правило, вся "фигуристость" здесь сводится к макетированию сетки кроссворда в виде какой-нибудь несложной фигуры: собачка, машинка, елочка, ракета и т.п. В остальном же это обычный классический кроссворд.
Гораздо реже встречается фигурные кроссворды другого типа: диагональные, сотовые, круговые и т.п. Почему? Да потому, что их труднее составлять. Чуть ниже показаны сетри трех таких "крученых" кроссворда:
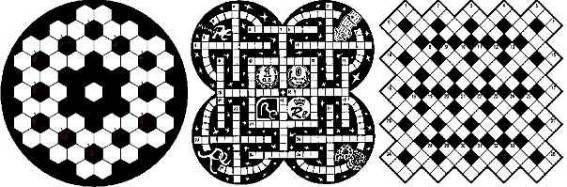

Примеры сеток фигурных кроссвордов
Пример сетки объемного кроссворда
Кроссворд "Объемный"
Тоже классический кроссворд, но уже с более сложной сеткой, чем у фигурных. Хитрость его заключается в том, что визуально такая сетка воспринимается как некая объемная фигура. Взгляните на пример сетки одного из таких кроссвордов, и вам все станет ясно и понятно:

